Answer:
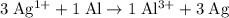 .
.
Step-by-step explanation:
Electrons are conserved in a chemical equation.
The superscript of
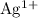 indicates that each of these ions carries a charge of
indicates that each of these ions carries a charge of
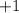 . That corresponds to the shortage of one electron for each
. That corresponds to the shortage of one electron for each
 ion.
ion.
Similarly, the superscript
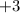 on each
on each
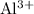 ion indicates a shortage of three electrons per such ion.
ion indicates a shortage of three electrons per such ion.
Assume that the coefficient of
 (among the reactants) is
(among the reactants) is
 , and that the coefficient of
, and that the coefficient of
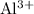 (among the reactants) is
(among the reactants) is
 .
.
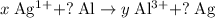 .
.
There would thus be
 silver (
silver (
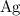 ) atoms and
) atoms and
 aluminum (
aluminum (
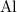 ) atoms on either side of the equation. Hence, the coefficient for
) atoms on either side of the equation. Hence, the coefficient for
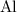 and
and
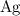 would be
would be
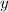 and
and
 , respectively.
, respectively.
 .
.
The

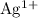 ions on the left-hand side of the equation would correspond to the shortage of
ions on the left-hand side of the equation would correspond to the shortage of
 electrons. On the other hand, the
electrons. On the other hand, the

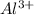 ions on the right-hand side of this equation would correspond to the shortage of
ions on the right-hand side of this equation would correspond to the shortage of
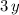 electrons.
electrons.
Just like atoms, electrons are also conserved in a chemical reaction. Therefore, if the left-hand side has a shortage of
 electrons, the right-hand side should also be
electrons, the right-hand side should also be
 electrons short of being neutral. On the other hand, it is already shown that the right-hand side would have a shortage of
electrons short of being neutral. On the other hand, it is already shown that the right-hand side would have a shortage of
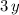 electrons. These two expressions should have the same value. Therefore,
electrons. These two expressions should have the same value. Therefore,
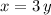 .
.
The smallest integer
 and
and
 that could satisfy this relation are
that could satisfy this relation are
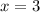 and
and
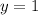 . The equation becomes:
. The equation becomes:
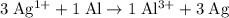 .
.