Answer:
(i).
 . Point
. Point
 is at
is at
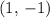 .
.
(ii). Point
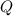 is at
is at
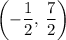 .
.
(iii).
 (slope-intercept form) or equivalently
(slope-intercept form) or equivalently
 (standard form.)
(standard form.)
Explanation:
Coordinates of the Extrema
Note, that when
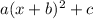 is expanded, the expression would become
is expanded, the expression would become
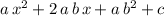 .
.
Compare this expression to the original
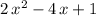 . In particular, try to match the coefficients of the
. In particular, try to match the coefficients of the
 terms and the
terms and the
 terms, as well as the constant terms.
terms, as well as the constant terms.
- For the
 coefficients:
coefficients:
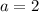 .
. - For the
 coefficients:
coefficients:
 . Since
. Since
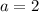 , solving for
, solving for
 gives
gives
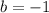 .
. - For the constant terms:
 . Since
. Since
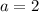 and
and
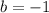 , solving for
, solving for
 gives
gives
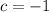 .
.
Hence, the original expression for the parabola is equivalent to
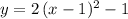 .
.
For a parabola in the vertex form
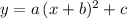 , the vertex (which, depending on
, the vertex (which, depending on
 , can either be a minimum or a maximum,) would be
, can either be a minimum or a maximum,) would be
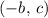 . For this parabola, that point would be
. For this parabola, that point would be
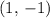 .
.
Coordinates of the Two Intersections
Assume
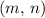 is an intersection of the graphs of the two functions
is an intersection of the graphs of the two functions
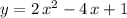 and
and
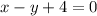 . Setting
. Setting
 to
to
 , and
, and
 to
to
 should make sure that both equations still hold. That is:
should make sure that both equations still hold. That is:
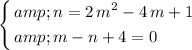 .
.
Take the sum of these two equations to eliminate the variable
 :
:
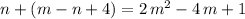 .
.
Simplify and solve for
 :
:
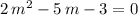 .
.
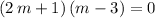 .
.
There are two possible solutions:
 and
and
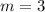 . For each possible
. For each possible
 , substitute back to either of the two equations to find the value of
, substitute back to either of the two equations to find the value of
 .
.
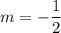 corresponds to
corresponds to
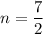 .
.
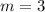 corresponds to
corresponds to
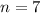 .
.
Hence, the two intersections are at
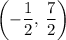 and
and
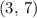 , respectively.
, respectively.
Line Joining Point Q and the Midpoint of Segment AP
The coordinates of point
 and point
and point
 each have two components.
each have two components.
- For point
 , the
, the
 -component is
-component is
 while the
while the
 -component is
-component is
 .
. - For point
 , the
, the
 -component is
-component is
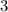 while the
while the
 -component is
-component is
 .
.
Let
 denote the midpoint of segment
denote the midpoint of segment
 . The
. The
 -component of point
-component of point
 would be
would be
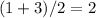 , the average of the
, the average of the
 -components of point
-components of point
 and point
and point
 .
.
Similarly, the
 -component of point
-component of point
 would be
would be
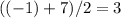 , the average of the
, the average of the
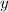 -components of point
-components of point
 and point
and point
 .
.
Hence, the midpoint of segment
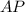 would be at
would be at
 .
.
The slope of the line joining
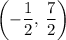 (the coordinates of point
(the coordinates of point
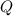 ) and
) and
 (the midpoint of segment
(the midpoint of segment
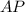 ) would be:
) would be:
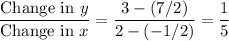 .
.
Point
 (the midpoint of segment
(the midpoint of segment
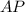 ) is a point on that line. The point-slope form of this line would be:
) is a point on that line. The point-slope form of this line would be:
 .
.
Rearrange to obtain the slope-intercept form, as well as the standard form of this line:
 .
.
 .
.