Answer:
£3263.98 (nearest penny)
Step-by-step explanation:
Compound interest formula
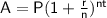
where:
- A = final amount
- P = principal
- r = interest rate (in decimal form)
- n = number of times interest applied per time period
- t = number of time periods elapsed
Given:
- P = £2900
- r = 3% = 0.03
- n = 1
- t = 4
Substituting given values into the formula and solving for A:
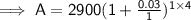
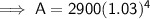
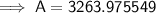
Therefore, Colin will have £3263.98 after 4 years (to the nearest penny).