Question

What is an equation of the line that passes through the points (4,-6) and (8,-4)​

Answer 1

`y = (1)/(2) x - 8`

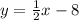
Explanation:

The equation of a line is usually written in the form of y=mx+c, where m is the gradient (also known as slope) and c is the y-intercept (the point through which the line cuts through the y-axis).

`\boxed{gradient = (y1 - y2)/(x1 - x2) }`

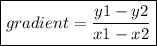
Using the gradient formula above,

`m = ( -4 - ( - 6))/(8 - 4) \\ m = ( - 4 + 6)/(4) \\ m = (2)/(4) \\ m = (1)/(2)`

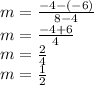
Substitute the value of m into the equation:

y= ½x +c

To find the value of c, substitute a pair of coordinates.

When x=4, y= -6,

-6= ½(4) +c

-6= 2 +c

c= -6 -2 (-2 on both sides)

c= -8 (simplify)

Thus, the equation of the line is y= ½x -8.