Question

A laser pointer used in the classroom emits light at 5650 Å, at a power of 4.00 mW. (One watt is the SI unit of power, the measure of energy per unit of time. 1 W = 1 J/s). How many photons are emitted from the pointer in 115 seconds?

Answer 1

1.308 x 10¹⁸ photons were emitted from the laser pointer.

Step-by-step explanation:

Given;

wavelength of the photon, λ = 5650 Å = 5650 x 10⁻¹⁰ m

power emitted by the source, P = 4 mW = 4 x 10⁻³ W

time of photon emission, t = 115 s

The energy of a single photon is given by;

E = hf

f = c / λ

`E = (h c )/(\lambda)`

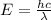
where;

c is speed of light = 3 x 10⁸ m/s

h is Planck's constant = 6.626 x 10⁻³⁴ Js

`E = ((6.626 *10^(-34)) (3*10^8) )/(5650*10^(-10))\\\\ E = 3.518*10^(-19) \ J`

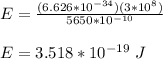
Energy of the source (laser pointer) = P x t

= (4 x 10⁻³ W) (115 s )

= 0.46 J

If no energy is lost, then emitted energy by the source must be equal to total energy of then photons;

`E_T = n E_(photon)\\\\n = (E_T)/(E_(photon))\\\\n = (0.46)/(3.518*10^(-19))\\\\n = 1.308*10^(18) \ photons`

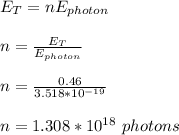
Therefore, 1.308 x 10¹⁸ photons were emitted from the laser pointer.

Answer 2

n = 1.3 x 10¹⁸ photons

Step-by-step explanation:

First we need to calculate the amount of energy released in given time:

E = Pt

where,

E = Energy = ?

P = Power = 4 mW = 0.004 W

t = time = 115 s

Therefore,

E = (0.004 W)(115 s)

E = 0.46 J

Now, this energy can be given in forms of photons as:

E = nhc/λ

where,

n = No. of photons = ?

h = Plank's Constant = 6.626 x 10⁻³⁴ J.s

c = speed of light = 3 x 10⁸ m/s

λ = wavelength of light = 5650 x 10⁻¹⁰ m

Therefore,

0.46 J = n(6.626 x 10⁻³⁴ J.s)(3 x 10⁸ m/s)/(5650 x 10⁻¹⁰ m)

n = (0.46 J)/(3.5 x 10⁻¹⁹ J)

n = 1.3 x 10¹⁸ photons