Answer:
(a) 99.7% of organs will be between 185 grams and 455 grams.
(b) 68% of organs weighs between 275 grams and 365 grams.
(c) The percentage of organs weighs less than 275 grams or more than 365 grams is 32%.
(d) The percentage of organs weighs between 230 grams and 365 grams is 81.5%.
Explanation:
The complete question is: The weight of an organ in adult males has a bell-shaped distribution with a mean of 320 grams and a standard deviation of 45 grams. Use the empirical rule to determine the following. (a) About 99.7% of organs will be between what weights? (b) What percentage of organs weighs between 275 grams and 365 grams? (c) What percentage of organs weighs less than 275 grams or more than 365 grams? (d) What percentage of organs weighs between 230 grams and 365 grams?
We are given that the weight of an organ in adult males has a bell-shaped distribution with a mean of 320 grams and a standard deviation of 45 grams.
Let X = the weight of an organ in adult males
So, X ~ Normal(
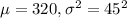 )
)
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean weight = 320 grams
= population mean weight = 320 grams
 = standard deviation = 45 grams
= standard deviation = 45 grams
Now, the empirical rule states that;
- 68% of the data values lies within one standard deviation from the mean.
- 95% of the data values lies within two standard deviation from the mean.
- 99.7% of the data values lies within three standard deviation from the mean.
(a) We have to find 99.7% of organs will be between what weights;
As we know that 99.7% of the data values lies within three standard deviation from the mean, that means;
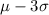 =
=
 = 185 grams
= 185 grams
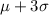 =
=
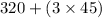 = 455 grams
= 455 grams
Hence, 99.7% of organs will be between 185 grams and 455 grams.
(b) The percentage of organs weighs between 275 grams and 365 grams is given by;
z score for 275 grams =

=
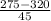 = -1
= -1
z score for 365 grams =

=
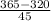 = 1
= 1
This means that 68% of organs weighs between 275 grams and 365 grams.
(c) The percentage of organs weighs less than 275 grams or more than 365 grams is given by;
As we see in the above part that 68% of organs weighs between 275 grams and 365 grams, this means that the percentage of organs weighs less than 275 grams or more than 365 grams will be = 1 - 68% = 0.32 or 32%.
So, the percentage of organs weighs less than 275 grams =
 = 16%
= 16%
and the percentage of organs weighs more than 365 grams =
 = 16%.
= 16%.
(d) The percentage of organs weighs between 230 grams and 365 grams is given by;
z score for 230 grams =

=
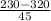 = -2
= -2
z score for 365 grams =

=
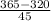 = 1
= 1
As we know that 95% of the data values lies within two standard deviation from the mean, that means 5% of the data lies outside 2 standard deviations.
So, the percentage of organs weight between 230 grams and the mean =
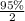 = 47.5%
= 47.5%
Similarly, 68% of the data values lies within one standard deviation from the mean, that means 32% of the data lies outside one standard deviation.
So, the percentage of organs weight between mean and 365 grams =
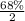 = 34%
= 34%
Hence, the percentage of organs weighs between 230 grams and 365 grams = 47.5% + 34% = 81.5%.