Question

An investment offers $9,600 per year for 16 years, with the first payment occurring one year from now. Assume the required return is 12 percent. a. What is the value of the investment today? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) b. What would the value be if the payments occurred for 41 years? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) c. What would the value be if the payments occurred for 76 years? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) d. What would the value be if the payments occurred forever? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.)

Answer 1

a) $66,949.44

b) $79,232.37

c) $79, 985.46

d) $80,000

Step-by-step explanation:

a) Value of return received per year = $9,600

Rate of interest = 12%

Period = 16 years

Thus, value of investment today shall be the discounted value of returns at the rate of 12%

= $9,600
`* ((1)/((1+0.12)^(1) ) + (1)/((1+0.12)^(2) ) + (1)/((1+0.12)^(3) ) + ..................... + (1)/((1+0.12)^(16) ))`

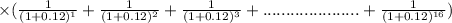
= $9,600
`*\ 6.9739`

= $66,949.44

b) Value of return received per year = $9,600

Rate of interest = 12%

Period = 41 years

Thus, value of investment today shall be the discounted value of returns at the rate of 12%

= $9,600
`* ((1)/((1+0.12)^(1) ) + (1)/((1+0.12)^(2) ) + (1)/((1+0.12)^(3) ) + ..................... + (1)/((1+0.12)^(41) ))`

= $79,232.37

c) Value of return received per year = $9,600

Rate of interest = 12%

Period = 41 years

Thus, value of investment today shall be the discounted value of returns at the rate of 12%

= $9,600
`* ((1)/((1+0.12)^(1) ) + (1)/((1+0.12)^(2) ) + (1)/((1+0.12)^(3) ) + ..................... + (1)/((1+0.12)^(76) ))`

= $79,985.46

d) Value of return received till infinite period

=
`(Amount)/(Rate\ of\ interest)\ =\ (9,600)/(0.12)\ =\ 80,000`

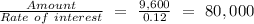
= $80,000