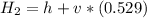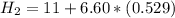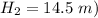Question

A hot air balloon is ascending straight up at a constant speed of 6.60 m/s. When the balloon is 11.0 m above the ground, a gun fires a pellet straight up from ground level with an initial speed of 30.0 m/s. Along the paths of the balloon and the pellet, there are two places where each of them has the same altitude at the same time. How far above ground level are these places

Answer 1

`H_1 =39.05 \ m` OR
`H_2 =14.5 \ m)`

Step-by-step explanation:

From the question we are told that

The constant speed of the balloon is
`v = 6.60 \ m/s`

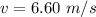
The height of the balloon is
`h = 11.0 \ m`

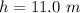
The initial speed of the pellet is
`u = 30 \ m/s`

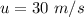
Generally the height of the balloon at the point it is the same altitude with the pellet is mathematically represented as

`H = h + v * (t)`

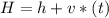
Note: vt is the distance covered by the balloon before the pellet got to it

Generally the height of the pellet when it is the same height with the balloon is mathematically represented using kinematics equation

`s = ut + (1)/(2) gt^2`

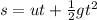
So

H = s

=>
`ut + (1)/(2) gt^2 = h + v * (t)`

=>
`30t + (1)/(2) *( -9.8)t^2 = 11 + 6.60t`

=>
`4.9t^2 -23.4t + 11= 0`

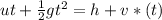
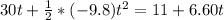
using the quadratic formula to solve the above equation

From the quadratic formula calculation

`t_1 = 4.25 \ s`

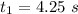
OR

`t_1 =  0.529  \  s`

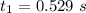
So the height of this two place above the ground is mathematically evaluated as

`H_1 = h + v * (4.25)`

`H_1 = 11 + 6.60 * (4.25)`

`H_1 =39.05 \ m`

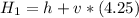
OR

`H_2 = h + v * ( 0.529)`

`H_2 = 11 + 6.60 * (0.529)`

`H_2  =14.5 \  m)`