Complete Question
A researcher is funded to obtain an estimate for the population proportion of smokers who have tried using e-cigarettes. She plans to interview 100 smokers. Previous studies have estimated that 20% of smokers have tried e-cigarettes. She finds that 23% of smokers have tried e-cigarettes.
Which of the following is correct?
A
0.23 is the population proportion
B
The margin of error for a 95% confidence interval is 8%
C
The standard error of the sample proportion is 0.177
D
This is a biased estimate because it is based on smokers none of the above
Answer:
The correct option is B
Step-by-step explanation:
From the question we are told that
The sample size is n = 100
The population proportion is p = 0.20
The sample proportion is
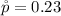
Generally the standard error is mathematically represented as
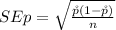
=>

=>
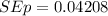
Generally for a 95% confidence level is level of significance is

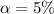

Now the critical value of
 obtained from the normal distribution table is
obtained from the normal distribution table is
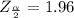
Generally the percentage margin of error is mathematically represented as