Question

Once filled to a volume of 1000 cm3 , the balloon leaks due to the diffusion of helium through the balloon material. The flux of helium across the balloon surface can be expressed as kC, where C is the concentration of gas inside the balloon and k is a mass transfer coefficient with a value of 1x10-7 cm/s. Determine how long it takes for the balloon to shrink to a volume of 500 cm3 . You may treat the balloon as spherical.

Answer 1

6.93 × 10⁶ s

Step-by-step explanation:

We know that the rate of gas leakage in the balloon is given by

dm/dt = -kCV where m = mass of gas, k = mass transfer coefficient = 1 × 10⁻⁷ cm/s, C = concentration of gas in balloon and V = volume of gas in balloon.

We know m = CV, so

dm/dt = dCV/dt = -kCV

CdV/dt = -kCV

dV/dt = -kV

Separating the variables, we have

dV/V = -kdt

Integrating both sides, we have

∫dV/V = -∫kdt

㏑V = -kt + C

V = exp(-kt)exp(C)

V =
`Ae^(-kt)`

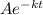
when t = 0, V = V₀

`V_(0) = Ae^(-k0)\\V_(0) = Ae^(0)\\V_(0) = A`

`V = V_(0) e^(-kt)`

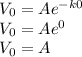
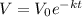
Now since V₀ = 1000 cm³ and we require the time when V = 500 cm³.

Substituting V and V₀ into the equation, we have

`500 = 1000 e^(-kt)\\500/1000 = e^(-kt)\\1/2 = e^(-kt)`

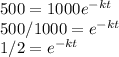
taking natural logarithm of both sides, we have

㏑(1/2) = -kt

t = -㏑(1/2)/k

substituting the value of k we have

t = -㏑(1/2)/1 × 10⁻⁷ cm/s

t = 0.693 × 10⁷ s

t = 6.93 × 10⁶ s