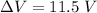Answer:
The value is
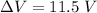
Step-by-step explanation:
From the question we are told that
The formula for the Electric potential difference is
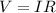
The current is
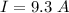
The uncertainty of the current is
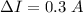
The Resistance is

The uncertainty of the Resistance is

Taking the log of both sides of the formula
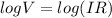
=>
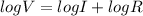
differentiating both sides
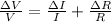
Here V is mathematically evaluated as
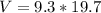
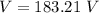
So from
![\Delta V = V * [(\Delta I)/(I) +(\Delta R)/(R) ]](https://img.qammunity.org/2021/formulas/physics/college/1vrhmnice809npuxzpjdaoa1azev2u2vb3.png)
![\Delta V = 183.21 [ (0.3 )/(9.3) + (0.6)/(19.7)]](https://img.qammunity.org/2021/formulas/physics/college/h08q60treq3gjxj7jvtzy4pkdds25wchec.png)
=>