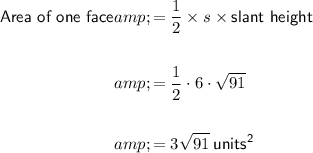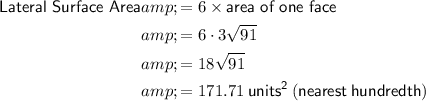Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.

Find the lateral area the regular pyramid.


LA. =

Answer 1

Lateral surface area =
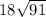`18√(91)` units²

= 171.71 units²

Explanation:

Lateral area: total surface area excluding its base

Find the radius (circumradius) of the regular hexagonal base. Use this to find the slant edge of the pyramid, then use the slant edge to find the slant height and thus the area of each face.

Radius of a regular polygon: distance from its center to its vertices.

`\textsf{Radius of a regular polygon}=(s)/(2 \sin \left((180^(\circ))/(n)\right))`

where:

• s = side length
• n = number of sides

Given:

• s = 6 units
• n = 6

`\implies \textsf{Radius}=(6)/(2 \sin \left((180^(\circ))/(6)\right))=6\:\sf units`

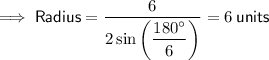
Use Pythagoras' Theorem to find the slant edge:

`\begin{aligned}\textsf{Slant edge} & =\sf √(r^2+h^2)\\& = √(6^2+8^2)\\ & = 10\:\sf units\end{aligned}`

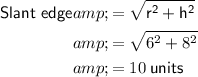
Use Pythagoras' Theorem to find the slant height:

`\begin{aligned}\textsf{Slant height} & = \sqrt{\textsf{slant edge}^2-\left((s)/(2)\right)^2}\\& =√(10^2-3^2)\\ & =√(91)\: \sf units\end{aligned}`

`\begin{aligned}\textsf{Area of one face} & = (1)/(2) * s * \textsf{slant height}\\\\ & = (1)/(2) \cdot 6 \cdot √(91)\\\\ & = 3√(91)\: \sf units^2\end{aligned}`

`\begin{aligned}\textsf{Lateral Surface Area}& = 6 * \textsf{area of one face}\\ & = 6 \cdot 3√(91)\\ & = 18√(91)\\ & =171.71\: \sf units^2\:(nearest\:hundredth)\end{aligned}`