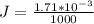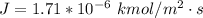Question

The gas CO2 is diffusing at steady state through a tube 0.20 meters long. The tube has a diameter of 0.01 meters and also contains N2 at 298 K. The total pressure inside the tube is constant at 101.32 kPa. The partial pressure of CO2 is 456 mm Hg at one end and 76 mm Hg at the other end. The diffusion coefficient of CO2 in N2 is 1.67 x 10-5 m2 /sec at 298 K. Calculate the molar flux of CO2 in SI units, assuming equimolar counter-diffusion between the CO2 and N2 gases.

Answer 1

The value is
`J = 1.71 *10^(-6) \ kmol/m^2\cdot s`

Step-by-step explanation:

From the question we are told that

The length the tube is
`l = 0.20 \ m`

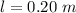
The diameter of the tube is
`d = 0.01 \ m`

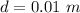
The total pressure inside the tube is
`P = 101.32\ kPa = 101.32 *10^(3) \ Pa`

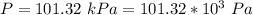
The partial pressure of CO2 at the first end is
`P_1 = 456 \ mmHg = 456 *133.322 = 60794.832 \ Pa`

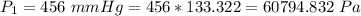
The partial pressure of CO2 at the other end is
`P_2 = 76 \ mmHg = 76 *133 = 10132.472 \ Pa`

The temperature is T = 298 K

The diffusion coefficient is
`D_(1,2) = 1.67 * 10^(-5) \ m^2 /s`

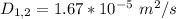
Generally the molar flux of CO2 is mathematically represented as

`J = (D_(1,2) * [P_1 -P_2])/(R* T[l])`

Here R is the gas constant with value
`R = 8.314 \ J/k mol`

So

`J = ( 1.67 * 10^(-5) * [60794.832 -10132.472 ])/(8.314 * 298 [0.20])`

`J = 1.71 *10^(-3) \ mol/m^2\cdot s`

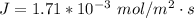
Converting to kmol

`J = (1.71 *10^(-3))/(1000)`

`J = 1.71 *10^(-6) \ kmol/m^2\cdot s`