Question

The initial mass of a certain species of fish is million tons. The mass of​ fish, if left​ alone, would increase at a rate proportional to the​ mass, with a proportionality constant of ​/yr. ​However, commercial fishing removes fish mass at a constant rate of million tons per year. When will all the fish be​ gone? If the fishing rate is changed so that the mass of fish remains​ constant, what should that rate​ be?

Answer 1

Answer:I think it’s 40 sorry if it’s wrong :/

Explanation:

Answer 2

The question is incomplete. Here is the complete question.

The initial mass of a certain species of fish is 7 millions tons. The mass of fish, if left alone, would increase at a rate proportional to the mass, with a proportionality constant of 2/yr. However, comercial fishing removes fish mass at a rate of 15 million tons per year.

(a) When will all fish be gone?

(b) If the fishing rate is changed so that the mass of fish remains constant, what should the rate be?

Answer: (a) t = 1.35 years.

(b) Rate = 14,000,000

Explanation:

(a) Initial mass is
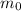`m_(0)` = 7,000,000

Rate of increase and comercial fishing gives an equation of growth:

`(dm)/(dt)=2m-15,000,000`

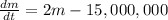
m' - 2m = - 15,000,000

This is an ordinary linear equation (ODE) of first order, of type:

y' + a(x)y = f(x)

where a(x) and f(x) are continuous.

To solve this type of linear equation, first calculate integrating factor, using:

`u(x) = e^{\int\limits {a(x)} \, dx }`

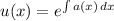
In our case,

`u(t) = e^{\int\limits {-2} \, dt }`

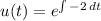
Solving:

`u(t) = e^(-2t )`

The general solution of a ODE can be written as

`y=(1)/(e^(u(x)))[\int\ {u(x).f(x)} \, dx + c]`

In our case:

`m=(1)/(e^(-2t))[\int\ {-2t.(-15)} \, dt + c]`

Solving:

`m=(1)/(e^(-2t))[(15)/(2)e^(-2t)+c ]`

To find constant c, use initial condition, i.e., m(0)=7,000,000:

`7,000,000=(1)/(e^(-2.0))[(15)/(2)e^(-2.0)+c ]`

`c=-500,000`

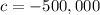
Then for the fish growth, general equation is:

`m=7500,000-500,000e^(2t)`

When the fish is gone, means m = 0, then:

`7500,000-500,000e^(2t)=0`

`500,000e^(2t)=7500,000`

`e^(2t)=15`

`ln(e^(2t))=ln(15)`

`t=(ln(15))/(2)`

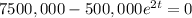
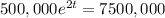
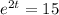
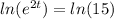
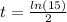
t = 1.35

It will take 1.35 years for the fish to be gone.

(b) For the mass to be constant, rate of growth must be zero:

`(dm)/(dt)=0`

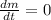
Suppose the changed fishing rate is k:

`2m_(0)-k=0`

`-k=-2.7,000,000`

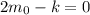
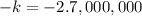
k = 14,000,000

To remain constant, rate must be 14,000,000.