Question

Nash Co. sells $435,000 of 12% bonds on June 1, 2020. The bonds pay interest on December 1 and June 1. The due date of the bonds is June 1, 2024. The bonds yield 8%. On October 1, 2021, Nash buys back $130,500 worth of bonds for $136,500 (includes accrued interest). Give entries through December 1, 2022. Prepare a bond amortization schedule using the effective-interest method for discount and premium amortization. Amortize premium or discount on interest dates and at year-end.

Answer 1

Journal entries:

cash 493,574.88 debit

bonds payable 435,000.00 credit

premium on bp 58,574.88 credit

--to record issuance--

Interest expense 19743

Amortization 6357

cash 26100

--to record Dec 31st, 2020--

Interest expense 19488.72

Amortization 6611.28

cash 26100

--to record June 30th, 2021--

bonds payable 130,500.00 debit

premium on bp 13,681.98 debit

interest expense 17,400.00 debit

gain on redemption 25,081.98 credit

cash 136,500.00 credit

--to record redemption--

premium on BP 4,813.04 debit

interest expense 13,456.96 debit

cash 18,270 credit

-- to record December 31st, 2021--

Step-by-step explanation:

First, we solve for the proceeds from the bonds payable:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 26,100 (435,000 x 12% / 2)

time 8 ( 4 years x 2)

yield to maturity 0.04 ( 8% / 2)

`26100 * (1-(1+0.04)^(-8) )/(0.04) = PV\\`

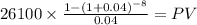
PV $175,724.6412

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 435,000.00

time 8.00

rate 0.04

`(435000)/((1 + 0.04)^(8) ) = PV`

PV 317,850.24

PV c $175,724.6412

PV m $317,850.2392

Total $493,574.8804

We now build the amortization schedule.

We take this value, we multiply by the interest rate and then, solve for amortization and ending carrying value.

To record the redemption:

accrued interest:

435,000 x 0.12 x 4/12 (months from June to oct) = 17,400

premium:

480,606.6 - 435,000 = 45,606.6

proportional of premium:

45,606 / 435,000 x 130,500 = 13.681,98

we now solve for the gain/loss on redemption:

130,500 + 13,681.98 + 17,400 = 161.581,9 value redeem

for cash 136,500

gain on redemption 25.081,98

bonds payable 130,500.00 debit

premium on bp 13,681.98 debit

interest expense 17,400.00 debit

gain on redemption 25,081.98 credit

cash 136,500.00 credit

Now, we solve for Dec 31st, 2021 entry.

bonds payable: 435,000 - 130,500 = 304,500

premium: 45,606 - 13,681.98 = 31.924,02

interest expense:

(304,500 + 31,924.02) x 0.04 = 13,456.96

cash outlay:

304,500 x 0.06 = 18,270

amortization 18,270 - 13,456.96 = 4,813.04