
Identify an equation in slope-intercept form for the line parallel to y = 4x - 9
that passes through (-5,3).
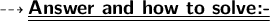
If lines are parallel to each other, they have the same slope.
If a line is parallel to
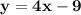 , and the slope of this line is 4, then the slope of the line that's parallel to
, and the slope of this line is 4, then the slope of the line that's parallel to
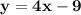 also has a slope of 4.
also has a slope of 4.
All right, we know the slope, but that's part of the slope-intercept equation,
We also need to identify the y-intercept; one way to find it (the one I always use) is the point-slope form.
Point-slope form looks like so:-
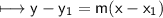
Replace y1 with 3, m with 4, and x1 with -5:-
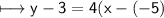
On simplification,

On further simplification,
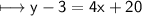
On further simplification,

Final equation:-
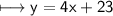
Good luck with your studies.
