Question

I NEED HELP WITH THIS ASAP!!

Answer 1

`\sf\huge {\dag Question }`

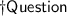
`\qquad \qquad` "Diagram"

Determine the value of m∠DCB.

`\sf\huge { \dag Solution }`

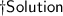
Here, in the diagram it is forming supplementary angle,

[The two angles that gives 180° when they add up are called]

So, we can conclude that,

`\sf { \angle DCA + \angle DCB = 180°}`

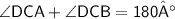
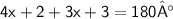`\sf { 4x + 2 + 3x + 3 = 180°}` [ Put the values and formed the suitable equation. ]

`\sf { \implies 4x + 3x + 2 + 3 = 180°}`

`\sf { \implies 7x + 5 = 180°}`

`\sf { \implies 7x = 180° - 5}`

`\sf { \implies 7x = 175}`

`\sf\red { \implies x = \cancel{(175)/(7)} = 25°}`

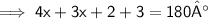
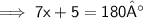
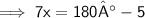
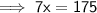
Value of x is 25°.

Now, put the value in the expression 3x + 3 (measurement of m∠DCB)

`\sf { \longrightarrow 3x +3}`

`\sf { \longrightarrow 3 * 25 +3}`

`\sf { \longrightarrow 75 +3}`

`\sf { \longrightarrow 78}`

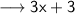
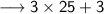
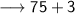
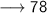
`\therefore` The value of m∠DCB is 78°.

________________________________

Answer 2

Answer: 78°

Explanation:

Looking at the picture, we can tell that ∠ACD and ∠DCB are supplementary angles. This means, they are equal to 180°. With that, we can find x and plug it into ∠DCB.

4x+2+3x+3=180 [combine like terms]

7x+5=180 [subtract both sides by 5]

7x=175 [divide both sides by 7]

x=25

Now that we know x=25, we can plug it in to find ∠DCB.

3(25)+3 [multiply]

75+3 [add]

78

Now, we know ∠DCB is 78°.