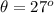Complete Question
The diagram illustrating this question is shown on the first uploaded image
Answer:
The value is
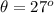
Step-by-step explanation:
Generally the distance covered by the ball thrown at angle 45° that did not bounce is mathematically represented as
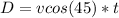
Here t is the total time duration which is mathematically represented as
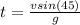
This distance distance is also mathematically represented as
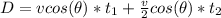
Here
 the angles made as shown in the diagram
the angles made as shown in the diagram
Here
 is the time before the first bounce which is mathematically represented as
is the time before the first bounce which is mathematically represented as

 is the time duration before the final point which is mathematically represented as
is the time duration before the final point which is mathematically represented as
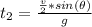
So

=>
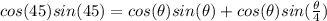
=>

=>