The question is incomplete. Here is the complete question.
Suppose that you are designing an instrument panel for a large industrial machine. The machine requires the person using it to reach 2 feet from a particular position. The reach from this position for adult women is known to have a mean of 2.8 feet with standard deviation of 0.5.The reach for adult men is known to have a mean of 3.1 feet with a standard deviation of 0.6. Both women's and men's reach from this position is normally distributed. If this design is implemented,
(a) What percentage of women will not be able to work on this intrument panel?
(b) What percentage of men will not be able to work on this intrument panel?
(c) Explain your answer to a person who has never had a course in statistics.
Answer: (a) 5.48%
(b) 3.36%
Explanation: For a normally distributed population, use z-score. The formula is
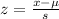
where
μ is the mean of the distribution
s is standard deviation
(a) For women, x = 2, μ = 2.8 and s = 0.5
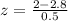
z = -1.6
Using z-score table
z = 0.548
Percentage of women not able to work on this instrument panel is 5.48%.
(b) For men, x = 2, μ = 3.1 and s = 0.6
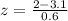
z = -1.83
Using the table
z = 0.336
Percentage of men not able to work on the panel is 3.36%.
(c) Z-score or standard score is defined as how far a data point is from the mean. It is a way to compare values in relation with a normal population.
So, having a population mean of 2, it is possible to determine how far from it a mean of women and a mean of men are.
With the results above, we can conclude that from all the workers designing the machine, 5.48% of women and 3.36% of men won't be able to work in the panel.