Question

A physics student standing on the edge of a cliff throws a stone vertically downward with an initial speed of 10.0 m/s. The instant before the stone hits the ground below, it is traveling at a speed of 30.0 m/s. If the physics student were to throw the rock horizontally outward from the cliff instead, with the same initial speed of 10.0 m/s, what is the magnitude of the velocity of the stone just before it hits the ground?

Answer 1

The magnitude of the stone velocity before it hits the ground is 30 m/s.

Step-by-step explanation:

Given;

initial vertical velocity,
`V_y_i = 10 \ m/s`

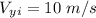
final vertical velocity,
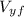`V_y_f` = 30 m/s

Apply the following kinematic equation to determine the height of the cliff;

`V_y_f^2 = V_y_i^2 + 2gh\\\\30^2= 10^2 + 2(9.8)h\\\\900 = 100 + 19.6h\\\\19.6h = 900 - 100\\\\19.6h = 800\\\\h = (800)/(19.6)\\\\h = 40.82 \ m`

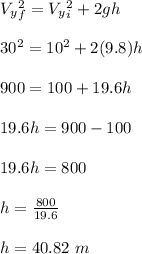
Determine time of the journey;

h = vₓ + ¹/₂gt²

vₓ = 0 (initial horizontal velocity when the stone was thrown vertically downward)

h = ¹/₂gt²

t = √ (2h / g)

t = √ (2(40.82) / 9.8)

t = 2.89 s

When the rock is projected horizontally, the horizontal distance, x = 40.82 m

Initial horizontal velocity,
`V_x_i = 10 \ m/s`

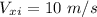
The final vertical component of the velocity is given by;

`V_f_y = V_y_i + gt\\\\V_f_y = 0 + 9.8(2.89)\\\\V_f_y = 28.32 \ m/s`

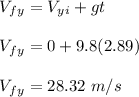
The magnitude of the stone velocity before it hits the ground is given by;

`V_f = √(V_x_i^2 + V_y_f^2) \\\\V_f = √(10^2 + 28.32^2)\\\\V_f = 30 \ m/s`

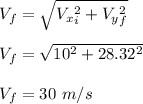
Therefore, the magnitude of the stone velocity before it hits the ground is 30 m/s.