A rectangular prism has a volume given by the expression (x^4+ 5x^3– 64x - 320) m^2 If the height of the prism is (x + 5) m, then determine the possible length and width of the …

Question

asked Dec 17, 2021 144k views

1 Answer

Kevin Hopps · Answer 1 · 2021-12-21T10:01:27+0000

Answer:

The possible length and width of the prism are
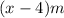(x-4)m and
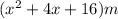(x^2+4x+16)m .

Explanation:

The base of the rectangular prism is rectangular. Let
and
be the length and width of the base.

Area of the base
= lw

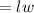
Given that the volume,

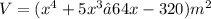V=(x^4+ 5x^3– 64x - 320) m^2 ,

and the height,

h= (x+5) m .

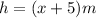The volume of the prism = (Area of the base) x (Height).i.e.

V=lwh

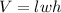
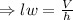
$\Rightarrow lw =(V)/(h)$

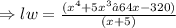
$\Rightarrow lw =((x^4+ 5x^3– 64x - 320))/((x+5))$

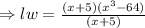
$\Rightarrow lw =((x+5)(x^3-64))/((x+5))$

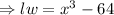
$\Rightarrow lw =x^3-64$

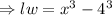
$\Rightarrow lw =x^3-4^3$

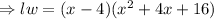$\Rightarrow lw =(x-4)(x^2+4x+16)$ [ using the identity
p^3-r^3=(p-r)(p^2+pr+r^2)]

Hence, the possible length and width of the prism are
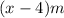(x-4)m and
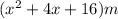(x^2+4x+16)m .