Answer:
The probability that his/her household has four or more cell phones in use is 0.122 or 12.2%.
Explanation:
The complete question is: In a survey of consumers aged 12 and older, respondents were asked how many cell phones were in use by the household. (No two respondents were from the same household.) Among the respondents, 215 answered "none", 280 said "one", 362 said "two", 149 said "three," and 140 responded with four or more. A survey respondent is selected at random. Find the probability that his/her household has four or more cell phones in use. Is it unlikely for a household to have four or more cell phones in use? Consider an event to be unlikely if its probability is less than or equal to 0.05.
We are given that among the respondents, 215 answered "none", 280 said "one", 362 said "two", 149 said "three," and 140 responded with four or more.
A survey respondent is selected at random.
As we know that the probability of any event is calculated as;
Probability =
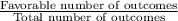
Here, we have to find the probability that his/her household has four or more cell phones in use;
Number of respondent having four or more cell phones in use = 140
Total number of respondents asked = 215 + 280 + 362 + 149 + 140 = 1146
So, the required probability =
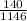
= 0.122 or 12.2%
No, it is not unlikely for a household to have four or more cell phones in use because the probability is not less than or equal to 0.05 but in actual it is greater than 0.05.