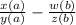Question

What is 4/5-1/6 with work shown​

Answer 1

Answer & Step-by-step explanation:

`(4)/(5)-(1)/(6)`

When you need to subtract fractions, the denominators (bottom) need to be the same. For this, you have to multiply both fractions until the bottom numbers are the same:

Find the lowest common multiple of the denominators:

`5,10,15,20,25,30\\6,12,18,24,30`

The LCM of 5 and 6 is 30. Now you have to multiply the top and bottom of the fractions until you get a denominator of 30*:

`(4(6))/(5(6))=(24)/(30)\\\\(1(5))/(6(5))=(5)/(30)`

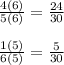
So,

`(24)/(30) -(5)/(30)`

When you subtract fractions, you only change the numerators (top). The denominator will stay the same:

`(24)/(30) -(5)/(30)=(19)/(30)`

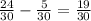
Since the fraction can't be further simplified,
`(4)/(5)-(1)/(6)=(19)/(30)`

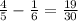
:Done

*When you are finding the same denominators, you need to multiply a single fraction's numerator and denominator by the same number. The two different fractions don't need to be multiplied by the same number:

`(x(a))/(y(a))-(w(b))/(z(b))`

Answer 2

the denominators need to be the same so if we multiply the first fraction by 6 and the second by 5, our new equation is

24/30 - 5/30

24-5=19

19/30 is your answer