Answer:
The answer is "
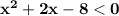 "
"
Explanation:
In this question, we calculates the roots value after compare with 0.
In the first point:
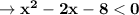
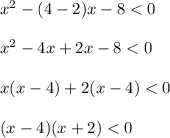
In the second point:
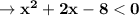
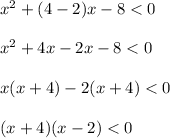
In the third point:
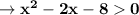
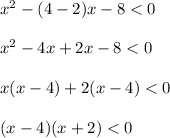
In the fourth point:
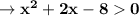
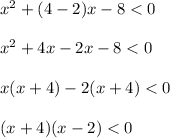
As there are roots -4 and 2, whether choice B and D is the answer. when measuring a point within the interval from -4 to 2, it is negative, that's why second choice is correct.