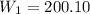The weight at an altitude of 1 mile above earths surface if he weighs 200 pounds on earth's surface is 200.10 pounds.
The relationship between weight (W), distance from the center of the Earth (d), and the radius of the Earth (r) can be expressed using the inverse square law:
![\[ W \propto (1)/(d^2) \]](https://img.qammunity.org/2021/formulas/mathematics/college/bh23kpo17sir9hyt8rbbtztesn1z216ns4.png)
Given that the radius of the Earth (r) is 3960 miles and the man weighs 200 pounds on the Earth's surface, we can set up a proportion to find the weight at an altitude of 1 mile above the Earth's surface.
Let
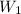 be the weight at 1 mile above the Earth's surface, and
be the weight at 1 mile above the Earth's surface, and
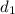 be the distance from the center of the Earth at that altitude.
be the distance from the center of the Earth at that altitude.
![\[ (W)/(W_1) = \left((d)/(d_1)\right)^2 \]](https://img.qammunity.org/2021/formulas/mathematics/college/wpm0gbdal433vhg2lzd6248yoynongoqul.png)
Given that
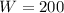 pounds and
pounds and
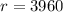 miles (radius of the Earth), and the altitude is 1 mile, we can substitute these values into the equation:
miles (radius of the Earth), and the altitude is 1 mile, we can substitute these values into the equation:
![\[ (200)/(W_1) = \left((3960)/(3961)\right)^2 \]](https://img.qammunity.org/2021/formulas/mathematics/college/msnw9oarh7d24s8ik1f8x9obz3mdrukrj7.png)
Now, solve for
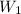 :
:
![\[ W_1 = (200)/(\left((3960)/(3961)\right)^2) \]](https://img.qammunity.org/2021/formulas/mathematics/college/kzfk24nbfruy4sahhmi6l811of46khs416.png)
Calculating this expression will give you the weight of the man at an altitude of 1 mile above the Earth's surface.