Question

An automobile is driven on a straight road, and the distance traveled by the automobile after time t=0 is given by a quadratic function s , where s(t) is measured in feet and t is measured in seconds for 0≤t≤12 . Of the following, which gives the best estimate of the velocity of the automobile, in feet per second, at time t=8 seconds?

Answer 1

See Explanation

Step-by-step explanation:

The question is incomplete as the value of s(t) is missing;

However, the following explanation will guide you;

I'll continue my explanation with the following assumption that:

`s(t) = 64 + 4(t-6)`

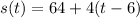
Required

Determine the velocity at t = 8

To do this; first calculate s(t) by substituting 8 for t in
`s(t) = 64 + 4(t-6)`

`s(8) = 64 + 4(8- 6)`

`s(8) = 64 + 4(2)`

`s(8) = 64 + 8`

`s(8) = 72`

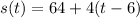
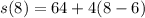
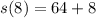
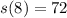
Next, is to calculate the velocity by dividing s(t) by t where t = 8

i.e.

`Velocity = (s(t))/(t)`

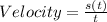
Substitute 8 for t

`Velocity = (s(8))/(8)`

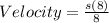
Substitute 72 for s(8)

`Velocity = (72)/(8)`

`Velocity = 9\ ft/s`

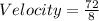
So: all you need to do is first calculate s(8), then divide the resulting value by 8 to get your result