Question

A girl throws a tennis ball with an initial speed of 20.0 m/s in the direction of 65.0° above the horizontal. She runs after the ball 0.30 s later from rest with a constant acceleration and then catches the ball at the same height. Ignore air resistance. (a) What is the maximum height (measured from the starting point) that the ball attains? (b) How long does it take for the girl (including the initial 0.30 s) to catch the ball? (c) How far has the ball gone horizontally when it is caught? (d) What is the acceleration of the girl during her run?

Answer 1

a) h = 16.7 m

b) t = 3.4 s

c) d = 31.3 m

d) a = 5.42 m/s²

Step-by-step explanation:

a) The maximum height can be calculated as follows:

`V_{f_(y)}^(2) = V_{0_(y)}^(2) - 2gh`

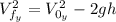
Where:

`V_{f_(y)}`: is the final speed in "y" direction = 0 (for maximum height)

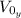`V_{0_(y)}`: is the initial speed in "y" direction

h: is the maximum height

g: is the gravity = 9.81 m/s²

`h = \frac{V_{0_(y)}sin(65)^(2)}{2g} = ((20*sin(65))^(2))/(2*9.81) = 16.7 m`

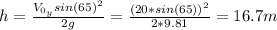
b) The time that will take for the girl to catch the ball is:

`h_(f) = h_(0) + V_{0_(y)}*t - (1)/(2)gt^(2)`

By solving the above equation for t we have:

`t = \frac{2V_{0_(y)}}{g} = (2*20*sin(65))/(9.81) = 3.70 s`

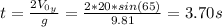
Since the girl runs after the ball 0.30 s later the total time is:

`t = 3.70 - 0.3 = 3.4 s`

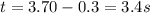
c) The distance in x can be found as follows:

`x = V_{0_(x)}*t = 20*cos(65)*3.7 = 31.3 m`

d) The acceleration of the girl is:

`x_(f) = x_(0) + V_{0_(x)}*t + (1)/(2)at^(2)`

By solving the above equation for "a" we have:

`a = (2*x_(f))/(t^(2)) = (2*31.3)/((3.4)^(2)) = 5.42 m/s^(2)`

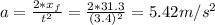
I hope it helps you!