Question

Avoiding an accident when driving can depend on reaction time. That time, measured in seconds from the moment the driver see danger until they step on the brake pedal, can be described by the Normal model �(1.5, 0.18). (15 pts) a) What percent of drivers have a reaction time less than 1.35 seconds? b) What percent of drivers have a reaction time greater than 1.9 seconds? c) What percent of drivers have a reaction time between 1.45 and 1.75 seconds? d) Describe the reaction time of the slowest 10% of all drivers? (hint: the slower a person reacts, the higher their reaction time) e) In what interval reaction times do the middle 60% of all drivers fall

Answer 1

The answer is below

Step-by-step explanation:

A normal model is represented as (μ, σ). Therefore for (1.5, 0.18), the mean (μ) = 1.5 and the standard deviation (σ) = 0.18

The z score shows by how many standard deviations the raw score is above or below the mean. It is given as:

`z=(x-\mu)/(\sigma)`

a) For x < 1.35 s

`z=(x-\mu)/(\sigma)\\\\z=(1.35-1.5)/(0.18)=-0.83`

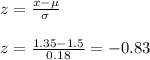
From the normal distribution table, the percent of drivers have a reaction time less than 1.35 seconds = P(x < 1.35) = P(z < -0.83) = 0.2033 = 20.33%

b) For x > 1.9 s

`z=(x-\mu)/(\sigma)\\\\z=(1.9-1.5)/(0.18)=2.22`

From the normal distribution table, the percent of drivers have a reaction time greater than 1.9 seconds = P(x > 1.9) = P(z > 2.22) = 1 - P(z<2.22) = 1 - 0.9868 = 0.0132 = 1.32%

c) For x = 1.45

`z=(x-\mu)/(\sigma)\\\\z=(1.45-1.5)/(0.18)=-0.28`

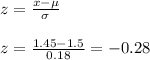
For x = 1.75

`z=(x-\mu)/(\sigma)\\\\z=(1.75-1.5)/(0.18)=1.39`

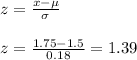
From the normal distribution table, P(1.45 < x < 1.75) = P(-0.28 < z < 1.39) = P(z < 1.39) - P(z< - 0.28) = 0.9177 - 0.3897 = 0.528 = 52.8%

d) A percentage of 10% corresponds to a z score of -1.28

`z=(x-\mu)/(\sigma)\\\\-1.28=(x-1.5)/(0.18)\\\\x-1.5=-0.2034\\\\x=1.27`

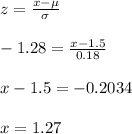
e) P(z < z1) - P(z< -z1) = 60%

P(z < z1) - P(z< -z1) = 0.6

P(z < -z1) = 1 - P(z < z1)

P(z<z1) - (1 - P(z < z1)) = 0.6

2P(z<z1) - 1= 0.6

2P(z<z1) = 1.6

P(z<z1) = 0.8

From the z table, z1 = 0.85

`0.85=(x-1.5)/(0.18)and-0.85=(x -1.5)/(0.18) \\\\x=1.65 \ and\ x=1.35`

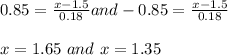
The reaction time between 1.35 and 1.65 seconds