Question

Which of the following ordered pairs belongs to the graph of f(x)

- 3x + 9?
O (1, – 10)
O (-1, 12)
O (2, – 3)
O (-2, 13)

Answer 1

The second choice,
`(-1,\, 12)`.

Explanation:

Note, that the expression
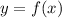`y = f(x)` is an equation. A point
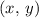`(x,\, y)` is on the graph of
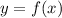`y = f(x)\!` if and only if the value of
`x` and
`y` satisfy this equation; that is: in other words, the
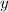`y\!`-coordinate of that point (the second number in the tuple) should be equal to
`f(x)`, which is equal to
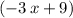`(-3\, x +9)` (evaluated where
`x\!` is equal to the first number in the tuple.

For each tuple in the choices, calculate the value of
`f(x)` where
`x` is equal to the first number of each tuple. Compare the result to the second number in that tuple. That choice corresponds to a valid point on
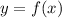`y = f(x)` only if these two numbers match.

• First choice:
  `x = 1`,
  `f(x) = f(1) = -3 + 9 = 6`. That's not the same as the second number,
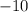  `-10`. Therefore, this point isn't on the graph of
  `y = f(x)`.
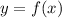• Second choice:
  `x = -1`,
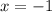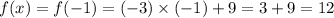  `f(x) = f(-1) = (-3)* (-1) + 9 = 3 + 9 = 12`. That matches the second number in the tuple. Therefore, this point is on the graph of
  `y = f(x)`.
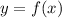• Third choice:
  `x = 2`,
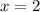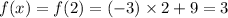  `f(x) = f(2) = (-3)* 2 + 9 = 3`. That's not the same as the second number,
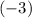  `(-3)`. Therefore, this point isn't on the graph of
  `y = f(x)`.
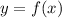• Fourth choice:
  `x = -2`,
  `f(x) = f(-2) = (-3)* (-2) + 9 = 15`. That's not the same as the second number,
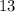  `13`. Therefore, this point isn't on the graph of
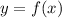  `y = f(x)`.