Answer:
The accuracy percentage for 50000 ft is 0.47%.
The accuracy percentage for 100000 ft is 0.92%.
Step-by-step explanation:
Given that,
Height = 50000 ft and 100000 ft
We need to calculate the new acceleration due to gravity
Using newtonian gravitational formula
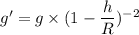
Where, g = acceleration due to gravity
h = height
R = radius
Put the value into the formula
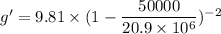
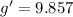
We need to find the accuracy percentage
Using formula for accuracy
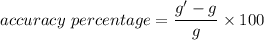
Put the value into the formula
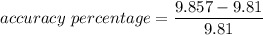
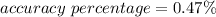
Now, For other height,
We need to calculate the new acceleration due to gravity
Using newtonian gravitational formula
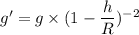
Put the value into the formula
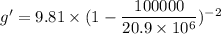
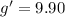
We need to find the accuracy percentage
Using formula for accuracy
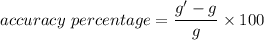
Put the value into the formula
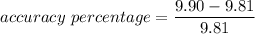
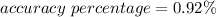
Hence, The accuracy percentage for 50000 ft is 0.47%.
The accuracy percentage for 100000 ft is 0.92%.