Question

West of a city, a certain eastbound route is straight and makes a steep descent toward the city. The highway has a 11% grade, which means that its slope is − 11 100 . Driving on this road, you notice from elevation signs that you have descended a distance of 1000 ft. What is the change in your horizontal distance in miles? (Round your answer to two decimal places.) mi

Answer 1

The change in horizontal distance is 1.72 mi

Explanation:

From the question, the highway has a 11% grade, which means that its slope is -11 / 100.

The negative sign indicates that the road is descending.

Hence, slope (m) = 11/100

The slope m, is given by

`Slope = (Rise)/(Run) = (\Delta y)/(\Delta x)`

Where Δy is the change in vertical distance and

Δx is the change in horizontal distance

Now, from the question, you have descended a distance of 1000 ft, that is

Δy = 1000 ft

Then, to determine the change in the horizontal distance Δx,

From

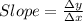`Slope = (\Delta y)/(\Delta x)`, then

`(11)/(100) = (1000ft)/(\Delta x)`

`11\Delta x = 1000ft * 100`

`\Delta x = (100000ft)/(11)`

∴
`\Delta x = 9090.91 ft`

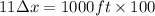
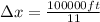
Δx = 9090.91 ft

This is the change in horizontal distance in ft, Now to convert it to miles

1 mile = 5280 ft

Hence, 1 ft = 1/5280 miles

If 1 ft = 1/5280 miles

Then, 9090.91 ft = x miles

x = 9090.91 × 1/5280

x = 1.72 miles

Hence, the change in horizontal distance in miles is 1.72 mi