Question

A 2010 study asserts that the number of hours that the average college student studies each week has been steadily dropping (The Boston Globe, July 4, 2010). In fact, the researchers state that, in the U.S., today’s undergraduates study an average of 14 hours per week. Suppose an administrator at a local university wants to show that the average study time of students at his university differs from the national average. He takes a random sample of 35 students at is university and finds that the average number of hours spent studying per week is 16.7. Assume that the population standard deviation is 7.2 hours. At 0.05 level of significance, what is the test statistics for testing the hypotheses H0: µ = 14 versus H1: µ ≠ 14?

Answer 1

Test statistic |Z| = |-2.21|

calculated value Z = 2.21 > 1.96 at 0.05 level of significance

Null hypothesis is rejected

The researchers state that, in the U.S., today’s undergraduates not study an average of 14 hours per week

Explanation:

Step(i):-

Given Mean of the Population' μ' = 14 hours per week

Given random sample size 'n'= 35

Mean of the sample (x⁻) = 16.7 hours per week

standard deviation of the Population (σ) = 7.2 hours per week

Level of significance = 0.05

Step(ii):-

Null hypotheses :H₁: µ = 14

Alternative Hypothesis : H₂: µ ≠ 14

Test statistic

`Z = (x^(-) -mean)/((S.D)/(√(n) ) )`

`Z = (14-16.7)/((7.2)/(√(35) ) )`

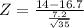
Z = -2.21

|Z| = |-2.21|

The tabulated value

Z₀.₀₅ = 1.96

calculated value Z = 2.21 > 1.96 at 0.05 level of significance

Null hypothesis is rejected

The researchers state that, in the U.S., today’s undergraduates not study an average of 14 hours per week