Answers:
Problem 1
- Domain =
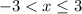 , interval notation (-3, 3]
, interval notation (-3, 3] - Range =
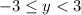 , interval notation [-3, 3)
, interval notation [-3, 3) - Is it a function? Yes
Problem 2
- Domain =
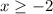 , interval notation
, interval notation
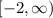
- Range = All real numbers, interval notation
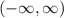
- Is it a function? No
Problem 3
- Domain =
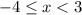 , interval notation [-4, 3)
, interval notation [-4, 3) - Range =
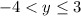 , interval notation (-4, 3]
, interval notation (-4, 3] - Is it a function? Yes
Problem 4
- Domain = All real numbers, interval notation
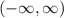
- Range =
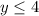 , interval notation
, interval notation
![(-\infty, 4]](https://img.qammunity.org/2021/formulas/mathematics/college/dpaz7vi92a08mlq8dn7964gxmbxy5yt962.png)
- Is it a function? Yes
==================================================
Explanations:
- The left most point is when x = -3, and we are not including this value due to the open hole. The other endpoint is included because it is a filled in circle. The domain is therefore
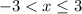 which in interval notation is (-3, 3]. We have the curved parenthesis meaning "exclude endpoint" and the square bracket says "include endpoint". The range is a similar story but we're looking at the smallest and largest y values. Though be careful about which endpoint is open/closed. We have a function because it passes the vertical line test.
which in interval notation is (-3, 3]. We have the curved parenthesis meaning "exclude endpoint" and the square bracket says "include endpoint". The range is a similar story but we're looking at the smallest and largest y values. Though be careful about which endpoint is open/closed. We have a function because it passes the vertical line test. - The smallest x value is x = -2. There is no largest x value because the arrows say to go on forever to the right. We can say the domain is
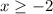 which in interval notation is
which in interval notation is
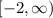 . The range is
. The range is
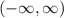 to indicate "all real numbers". This graph fails the vertical line test, so it is not a function. The vertical line test is where we check to see if we can pass a vertical line through more than one point on the curve. In this case, such a thing is possible which is why it fails the test.
to indicate "all real numbers". This graph fails the vertical line test, so it is not a function. The vertical line test is where we check to see if we can pass a vertical line through more than one point on the curve. In this case, such a thing is possible which is why it fails the test. - This is the same idea as problem 1, though note the endpoints are flipped in terms of which has an open circle and which doesn't. It is not possible to draw a single vertical line to have it pass through more than one point on the curve, so it passes the vertical line test and we have a function.
- This is a function because it passes the vertical line test. The domain is the set of all real numbers due to the arrows in both directions. Any x value is a possible input. The range is
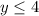 which is the same as saying
which is the same as saying
![(-\infty, 4]](https://img.qammunity.org/2021/formulas/mathematics/college/dpaz7vi92a08mlq8dn7964gxmbxy5yt962.png) in interval notation. This is because y = 4 is the largest y value possible. There is no smallest y value due to the arrows.
in interval notation. This is because y = 4 is the largest y value possible. There is no smallest y value due to the arrows.