Question

A high-speed steel tool is used to turn a steel work part with length = 350 mm and diameter = 70 mm. The parameters in the Taylor equation are n = 0.13 and C = 75 (m/min) for a feed of 0.4 mm/rev. The operator and machine tool rate = $36.00/hr, and the tooling cost per cutting edge = $4.25. It takes 5.0 min to load and unload the work part and 4.0 min to change tools. Determine the cutting speed for minimum cost.

Answer 1

42.85 m/min

Step-by-step explanation:

To save cost, the tools should not be changed frequently if the tool cost or tool change time is high

`The\ operator\ and\ machine\ tool\ rate =C_o=\$36/hr=(\$36)/(1\ hr*(60\ min)/(1\ hr) ) =\$0.6/min`

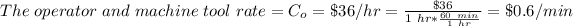
The tooling cost per cutting edge =
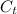`C_t` = $4.25

n = 0.13, C=75 (m/min), tool change time =
`t_t=4\ min`

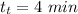
Therefore the cutting speed for minimum cost is given as:

`v_(max)=(C)/([(C_o)/(((1)/(n)-1 )(C_o*t_t+c_t)) ]^n) \\\\Substituting:\\\\v_(max)=75{[(0.6)/(((1)/(0.13)-1 )(0.6*4+4.25)) ]^(0.13)} \\\\v_(max)=42.85\ m/min`