Problem 5
Answers:
- Domain =
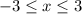 which in interval notation is [-3, 3]
which in interval notation is [-3, 3] - Range =
 which is also [-3, 3] in interval notation
which is also [-3, 3] in interval notation - Is it a function? Yes
-----------------
Step-by-step explanation:
The domain is the set of allowed x values. Here we see that x = -3 is the smallest possible x value and x = 3 is the largest. So x is anything between -3 and 3, including both endpoints. We write
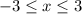 to indicate this. That converts to [-3,3] in interval notation. The square brackets mean "include this endpoint".
to indicate this. That converts to [-3,3] in interval notation. The square brackets mean "include this endpoint".
The range is the same story, but with the y values. Coincidentally, the range has the same exact endpoints as the domain does. This won't always be the case.
This graph is a function because it is not possible to draw a single vertical line through more than one point on the relation curve. Any x value pairs with one and only one y value. The next problem is a different story.
==========================================================
Problem 6
Answers:
- Domain =
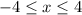 which in interval notation is [-4, 4]
which in interval notation is [-4, 4] - Range =
 and that is [-3,3] in interval notation
and that is [-3,3] in interval notation - Is it a function? No
----------------------------
Step-by-step explanation:
We use the same idea as before. The left most point tells us the smallest x value, and the right most point tells us the largest x value. The domain is everything in this interval including both endpoints. The range is a similar story but we're looking for the lowest and highest points to get the smallest and largest y values respectively.
This relation is not a function because this graph fails the vertical line test. It is possible to pass a single straight vertical line through more than one point on this curve. For example, draw a vertical line through x = 2 and it crosses the circle twice. This means the input x = 2 leads to more than one output, but a function must have exactly one output for any valid domain input value.