Answer:
(a) Maximum slope
 ,
,
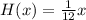
(b) 12.5 in.
Explanation:
The given condition is the wheelchair ramp must have a maximum rise of 1 in. for every horizontal distance of 12 in.
(a) Let m be the maximum allowable slope for the ramp.

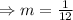 .
.
Let x be the distance in the horizontal direction as shown in the figure.
So, for slope m, the linear function H for the height is
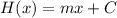 , where C is constant.
, where C is constant.
Now, at the starting of the ramp, x=0, and H=0.
Putting this condition back to the equation, we have
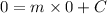
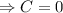 .
.
Hence, the required equation is
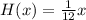
(b) The ramp is 150 in. wide,
So, height gained by the ramp at the end is,
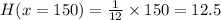 in.
in.