Question

Grades on a standardized test are known to have a mean of 1000 for students in the United States. The test is administered to 453 randomly selected students in Florida; in this sample, the mean is 1013, and the standard deviation (s) is 108. a. Construct a 95% confidence interval for the average test score for students in Florida. b. Is there statistically significant evidence that students in Florida perform differently from other students in the United States

Answer 1

a

The 95% confidence interval is
`1003 < \mu <1023`

b

Yes there is statistically significant evidence that students in Florida perform differently from other students in the United States

Explanation:

From the question we are told that

The population mean is
`\mu = 1000`

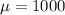
The sample size is
`n = 453`

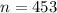
The sample mean is
`\= x = 1013`

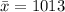
The standard deviation is
`s = 108`

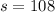
Given that the confidence level is 95% then the level of significance is mathematically represented as

`\alpha = 100 - 95`

=>
`\alpha = 5\%`

=>
`\alpha = 0.05`

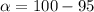
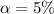
The critical value for
`(\alpha )/(2)` obtained from the normal distribution table is

`Z_{(\alpha )/(2) } = 1.96`

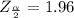
Generally the margin of error is mathematically represented as

`E = Z_{(\alpha )/(2) } * (s)/(√(n) )`

=>
`E = 1.96 * (108)/(√(453) )`

=>
`E = 9.946`

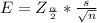
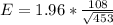
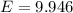
Generally the 95% confidence interval is mathematically represented as

`\= x - E < \mu < \= x + E`

=>
`1013 - 9.946 < \mu < 1013 + 9.946`

=>
`1003 < \mu <1023`

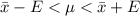
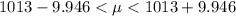
Given that the population mean(1000) is not within the 95% confidence interval for l for the average test score for students in Florida, then it means that there is statistically significant evidence that students in Florida perform differently from other students in the United States