Answer:
The uncertainty in the average speed is 0.134 meters per second.
Explanation:
Let be
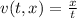 the average speed function, we calculate the uncertainty in the average speed by total differentials, which is in this case:
the average speed function, we calculate the uncertainty in the average speed by total differentials, which is in this case:
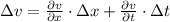
Where:
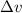 - Uncertainty in the average speed, measured in meters per second.
- Uncertainty in the average speed, measured in meters per second.
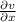 - Partial derivative of the average speed function with respect to distance, measured in
- Partial derivative of the average speed function with respect to distance, measured in
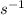 .
.
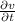 - Partial derivative of the average speed function with respect to time, measured in meters per square second.
- Partial derivative of the average speed function with respect to time, measured in meters per square second.
 - Uncertainty in distance, measured in meters.
- Uncertainty in distance, measured in meters.
 - Uncertainty in time, measured in seconds.
- Uncertainty in time, measured in seconds.
Partial derivatives are, respectively:
 ,
,
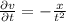
Then, the total differential expression is expanded as:

If we get that
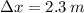 ,
,
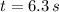 ,
,
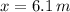 and
and
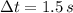 , the uncertainty in the average speed is:
, the uncertainty in the average speed is:
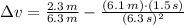
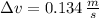
The uncertainty in the average speed is 0.134 meters per second.