Question

*. If (2,3) and (-6,5) are the end points of diagonal of a square. Find the equation of another diagonal.

Please help with this question..​

Answer 1

Answer: y = 4x + 12 (edited to reflect a SQUARE)

Explanation:

Opposite Diagonal of a square means the line goes through the midpoint and has the opposite reciprocal slope.

Use the Midpoint formula:
`M=\bigg((x_1+x_2)/(2),(y_1+y_2)/(2)\bigg)`

`M=\bigg((2-6)/(2),(3+5)/(2)\bigg)\\\\\\.\ =\bigg((-4)/(2),(8)/(2)\bigg)\\\\\\.\ =(-2,4)`

Use the Slope formula:
`m=(y_2-y_1)/(x_2-x_1)`

`m=(3-5)/(2+6)\quad =\quad (-2)/(8)\quad =\quad -(1)/(4)`

Opposite Diagonal slope is opposite (change the sign) and reciprocal (flip the fraction) → m⊥ = + 4

Now use the Point-Slope formula: y - y₁ = m⊥(x - x₁) where

• (x₁, y₁) is the midpoint (-2, 4)
• m = 4

y - 4 = 4(x + 2)

y - 4 = 4x + 8

y = 4x + 12

Answer 2

Simple question

slope of on le diagonal,whose coordinates are given=

`(y2 - y1)/(x2 - x1) = (5 - 3)/( - 6 - 2) = (2)/( - 8) or \: ( - 1)/(4)`

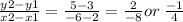
now we know that diagonals of square are perpendicular to each other

and we also know that if there are two perpendicular lines have slope m1 and m2 respectively,then

`m1 = ( - 1)/(m2)`

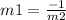
so if one diagonal's slope is -1/4 then other diagonal's slope will be 4

now we know that all the equation of a line is in the form

y=mx+c

where m is slope

so simply put the value of m=4

y=4x+c...i)

we also know that the line of equationi) will pass through the midpoint coordinates of first diagonal

mid point of first diagonal ={(2-6)/2 ,(5+3)/2}=(-2,4)

put this value of x and y in i) equation

4=-8+c

c=12

hence putting the value of c in equation I) we get the equation of line as

y=4x+12

y-4x-12=0