- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

The quotient of b and 3 is greater than or equal to 19.
✥First, the word "quotient" indicates that we divide.
Here we have "the quotient of b and 3", so we divide b by 3:-

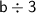
Now, this expression is greater than or equal to 19:-
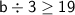
How to Solve for b
✳︎ Multiply by 3 on both sides:-
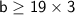
On simplification,

So the values of b greater than or equal to 57 will make this inequality true.
Let's solve another one.
✳︎ A number y increased by 5 is at least -21.
First, "increased" means we add 5.
Since y is increased by 5, we add 5 to y:-
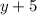
Now this expression is at least -21, which means it can't be less than -21, thus, it's greater than or equal to -21, which looks as follows:-
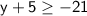

[Solving for y]
Subtract 5 on both sides:-
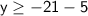
On simplification,

So the values of y greater than or equal to -26 will make this inequality true.
Good luck with your studies.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -