Answer:
pH = 1.39
Step-by-step explanation:
Given that:
The molarity of
 = 0.15 M
= 0.15 M
with acid dissociation constant
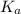 =
=
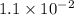
Acid dissociation constant of HClO =
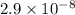
Molarity of HClO = 0.15 M
The objective is to determine the pH of the solution:\
To determine the concentration of
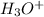 obtained from both acids
obtained from both acids
The equation for the reaction can be expressed as :
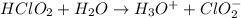
The dissociation constant for the above reaction is as follows:
![ka = \frac{ [H_3O^+] [ClO_2^-]} { [HClO_2]}](https://img.qammunity.org/2021/formulas/chemistry/college/e1ru1elhi04i7xkepqs4fintx09y2y7azs.png)
![1.1 * 10^(-2) = \frac{ [x] [x]} { [0.15]}](https://img.qammunity.org/2021/formulas/chemistry/college/nxln8aoue8mie8d69852q78pky0qivl65k.png)
![1.1 * 10^(-2) = \frac{ [x]^2 } { [0.15]}](https://img.qammunity.org/2021/formulas/chemistry/college/6v72va4arhimq73khuf4ycaqf1hc6cjs8z.png)

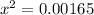
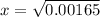
x = 0.04062 M
Now to determine the concentration of
 obtained from HClO
obtained from HClO
The equation for the reaction can be expressed as :
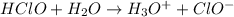
![ka = ([H3O^+] [ClO^-])/( [HClO])](https://img.qammunity.org/2021/formulas/chemistry/college/23n3com0ha9uluxjeykovhmc7voovi5phu.png)
![2.9 * 10 ^(-8) = ([x] [x])/( [0.15])](https://img.qammunity.org/2021/formulas/chemistry/college/j8p1lovm0jnty118k8s9omgj91zz2y2gs7.png)
![2.9 * 10 ^(-8) * [0.15] = {[x]^2}](https://img.qammunity.org/2021/formulas/chemistry/college/kqv3pyt2hm4n2szo1bjo8bhb5fh3pr3keu.png)
![{[x]} ^2=4.35 * 10^(-9)](https://img.qammunity.org/2021/formulas/chemistry/college/s2bqkfayi913b7do2w2wkzm8zg182guncc.png)
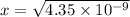

Thus the total concentration now is :
x =
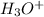 =
=
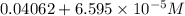
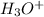 = 0.04068595 M
= 0.04068595 M
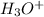
 0.04069 M
0.04069 M
pH = -log [H3O⁺]
pH = -log [0.04069]
pH = 1.39