Question

Find the vertex and y intercept of the quadratic function​

Answer 1

Answer: 5) Vertex = (2, 28) y-intercept = 40 → (0, 40)

6) Vertex = (2, 11) y-intercept = 7 → (0, 7)

Explanation:

The y-intercept of the equation is when x = 0. It is the c-value when given in standard form: y = ax² + bx + c

To find the vertex, use the Axis of Symmetry equation to find the x-value

x = -b/(2a). Then plug the x-value into the equation to find the y-value.

5) y = 3x² - 12x + 40

↓ ↓ ↓

a=3 b= -12 c=40

`\text{AOS:}\quad x=(-b)/(2a)\quad =(-(-12))/(2(3))\quad =(12)/(6)\quad =2`

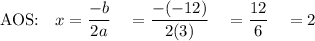
Min: y = 3(2)² - 12(2) + 40

= 3(4) - 24 + 40

= 12 - 24 + 40

= 28

Vertex: (2, 28) y-intercept = 40

*******************************************************************************************

6) y = -x² + 4x + 7

↓ ↓ ↓

a= -1 b=4 c=7

`\text{AOS:}\quad x=(-b)/(2a)\quad =(-(4))/(2(-1))\quad =(-4)/(-2)\quad =2`

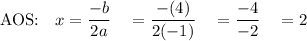
Max: y = -(2)² + 4(2) + 7

= -(4) + 8 + 7

= -4 + 8 + 7

= 11

Vertex: (2, 11) y-intercept = 7