Question

Each of the functions below model the monetary value of an item. Which is the only

that has a growth factor showing the item is increasing in value?

O a(x) = 90(3/4)^x

B(x) = 215(5/4)^x

c(x) = 73(0.98)^x

d(x) = 12(0.24)^x

Answer 1

The correct answer is
`b(x) = 215\cdot \left((5)/(4) \right)^(x)`.

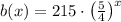Explanation:

We must remember that each option represents a geometrical progression, whose model is represented by:

`y = a\cdot r^(x)`

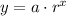
Where:

`y` - Dependent variable, dimensionless.

`a` - Initial value, dimensionless.

`r` - Common ration, dimensionless.

A geometric function is decreasing and monotone when
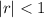`|r| < 1`, stable when
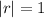`|r| = 1` and increasing and divergent when
`|r| > 1`.

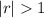The equation
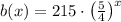`b(x) = 215\cdot \left((5)/(4) \right)^(x)` is the only one that is increasing in value, as notice that
`|r| = (5)/(4)> 1`. Therefore, the correct answer is B.