Answer:
Slope intercept form: y = -
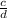 x +
x +
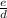
Explanation:
Given the general equation;
cx + dy = e
To make y the subject of the formula;
dy = e - cx
Divide through by d, to have;
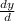 =
=
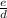 -
-
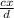
So that,
y =
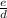 -
-
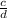 x
x
y = -
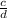 x +
x +
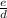
Thus, slope = -
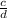 , and intercept =
, and intercept =
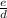
Therefore, a general form of the given equation is y = -
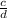 x +
x +
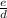 .
.