Answer:
The value of U = 4
The value of W = -6
The value of V = 5
The value of Z = 1
The value of x = 3
The value of y =2
Explanation:
Given:
20a³b³ – 24a⁵b² + 4a³b²
Solution:
Lets first factorize this expression:
20a³b³ – 24a⁵b² + 4a³b²
= −24a⁵b² + 20a³b³ +4a³b²
Taking 4a³b² common
= 4a³b² (−6a² + 5b + 1) ___ (1)
Now you can see this expression takes the form:
Ua^xb^y (Wa^2 + Vb+ z), where U > 0.
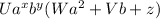
Now you can clearly see from (1)
The value of U is 4
The value of W is -6
The value of V is 5
The value of Z is 1
The value of x is 3
The value of y is 2
However if we take minus common from above equation:
20a³b³ – 24a⁵b² + 4a³b²
= −24a⁵b² + 20a³b³ +4a³b²
Taking 4a³b² common
= - 4a³b² (6a² - 5b - 1) ___ (1)
In this case the value of U is - 4, W is 6 , V is -5, Z is -1 , x is 3 and b is 2