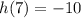Question

Find a linear function h, given h(8)=-12 and h(-1)=6. Then find h(7)

Answer 1

The linear function is
`h = -2\cdot x + 4`.
`h(7) = -10`

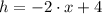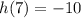
Explanation:

Any linear function is represented by a first-order polynomial, whose form is:

`h = m\cdot x + b`

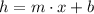
Where:

`h` - Independent variable, dimensionless.

`y` - Dependent variable, dimensionless.

`m` - Slope, dimensionless.

`b` - y-Intercept, dimensionless.

From Analytical Geometry we know that slope can be obtained from two distinct points lying on the linear function:

`m = (h_(2)-h_(1))/(x_(2)-x_(1))`

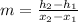
If we know that
`x_(1) = -1`,
`h_(1) = 6`,
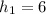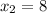`x_(2) = 8` and
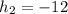`h_(2) = -12`, then the slope is:

`m = (-12-6)/(8-(-1))`

`m = -2`

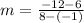
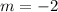
Now, we determine the y-intercept in linear function formula: (
`m = -2`,
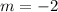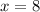`x= 8` and
`h = -12`)

`-12 = -2\cdot (8)+b`

`-12 = -16 + b`

`b = 4`

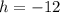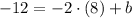
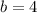
The linear function is
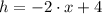`h = -2\cdot x + 4`. Finally, we evaluate the expression at
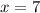`x = 7`:

`h (7) = -2\cdot (7) + 4`

`h(7) = -10`