Answer:
Explanation:
Given that the differential equation is:
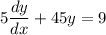
by dividing both sides by 5; we have:
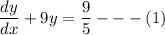
which is a form of a linear equation.
The integrating factor is:
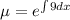
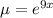
multiplying eqution (1) with
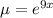

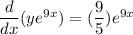
Using integration on both sides.
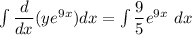
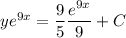
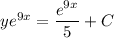
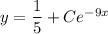
Thus, the general solution is :
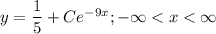
In general solution:
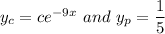
To talk of larger values of x, the value of
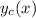 is said to be negligible.
is said to be negligible.
This implies that:
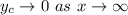
Thus,
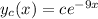 signifies a transient term in the general solution.
signifies a transient term in the general solution.