Question

Four points lie in a plane so that no three of them lie on a line. If lines are drawn connecting all pairs of these points, how many such lines are there?

Answer 1

6

Explanation:

Given that 4 points lie in a plane so that no 3 points of them lie on a line.

Let A, B, C, and D are four points as shown in the figure.

One line to be drawn, only 2 points are needed.

As no 3 points are collinear, so the number of combination of 2 points among the total 4 points gives the number of lines can be drawn.

As the total number of combinations of
`r` elements, taken at a time, among
`n` elements are

.

So, the required number of lines

`=\binom{4}{2}=(4!)/(2!*(4-2)!)=(4!)/(2!*2!)=(4*3*2*\1)/(2*1*2*1)=6`

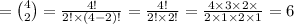
All the 6 possible lines can be verified from the figure.