![[|z - 3|^2 + |z - 5 + 2i|^2 + |z - 1 + i|^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/3fowdcyq2rppsmwxcesoso4iygmcvvebp7.png)
Let , complex number z be , z = x + iy .
Putting z in above equation , we get :
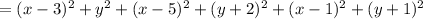
Now , getting critical points by :
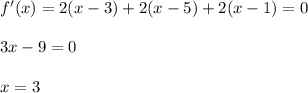
Also ,
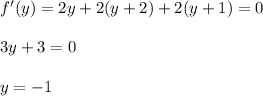
So , at point ( 3, -1 ) complex number given expression have minimum value.
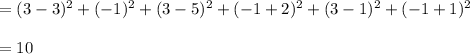
Therefore, minimum value is 10.
Hence, this is the required solution.