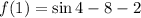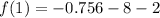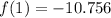Question

Given f''(x) = - 16 sin(4x) and f'(0) = - 4 and f(0) = - 2.

Findf(1) =

Answer 1

The complete equation is
`f(x) = \sin 4x -8\cdot x -2`.
`f(1) = -10.756`

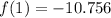
Explanation:

Let be
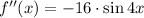`f''(x) = -16\cdot \sin 4x`, we need to determine the formula of
`f(x)` by integrating twice:

`f'(x) = \int {(-16\cdot \sin 4x)} \, dx`

`f'(x) = -16\int {\sin 4x} \, dx`

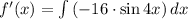
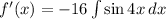
We apply the following algebraic substitution in expression above:

`u = 4\cdot x` and
`du = 4\,dx`

`f'(u) = -4\int {\sin u} \, du`

`f'(u) = 4\cdot \cos u + C_(1)`

`f'(x) = 4\cdot \cos 4x + C_(1)`

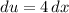
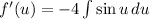
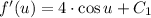
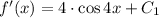
We use the same approach to determine
`f(x)`:

`f(x) = \int {(4\cdot \cos 4x)} \, dx + \int {C_(1)} \, dx`

`f(u, x) = \int {\cos u} \, du + C_(1)\int \, dx`

`f(u,x) = \sin u + C_(1)\cdot x + C_(2)`

`f(x) = \sin 4x + C_(1)\cdot x + C_(2)`

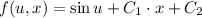
If we know that
`f'(0) = -4` and
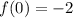`f(0) = -2`, the integration constants are obtained below:

`4 + C_(1) = -4`

`C_(1) = -8`

`C_(2) = -2`

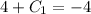
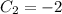
The complete equation is
`f(x) = \sin 4x -8\cdot x -2`. (Angles are measured in radians) Then:

`f(1) = \sin 4 - 8- 2`

`f(1) = -0.756-8-2`

`f(1) = -10.756`